Metoder i Matematik
De to overordnede metoder i matematik er den axiomatisk deduktive metode og modellering. Her gives en kort forklaring og konkrete eksempler på brug af metoderne. Yderligere uddybning af metoder i matematik kan findes i [3] (hvor statistisk modellering dog er i kategori for sig selv).
Axiomatisk deduktiv
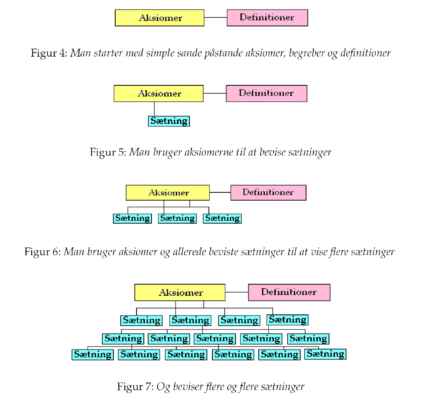
Ud fra grundsætninger (aksiomer) og definitioner kan sætninger og hjælpesætninger bevises, se Figur 1.
Hvis \(a = b\) og \(b = c\) så er \(a = c\).
Modellering
Vha. den matematiske teori kan der opstilles modeller ud fra et givent datamateriale eller antagelser. Disse modeller kan så bruges til nærmere undersøgelse og til at drage konklusioner for det der modelleres. Det kan fx udføres vha. regression og/eller differentialligninger.
Se de tre trin i figuren fra modelleringskompetencen i [1].
Konkret brug af metoderne
Man bruger sine matematiske kompetencer til at arbejde med metoderne. Herunder er eksempler på konkrete handlinger man ofte udfører som en del af den overordnede metode:
- oversætter almindeligt sprog til symbolsprog – og modsat
- håndterer formler og beskriver variabelsammenhænge
- løser ligninger
- anvender IT til at løse matematiske problemer
- forholder sig til modellers begrænsninger
- anvender statistik til at beskrive et givet datamateriale eller fænomener
- anvender funktionsanalyse i opstilling af matematiske modeller
- opstiller og løser geometriske modeller
- gør brug af matematiske ræsonnementer fx i bevisførelse